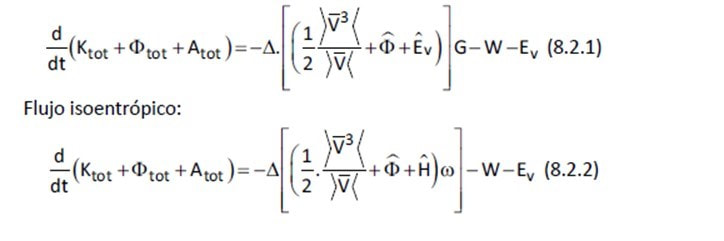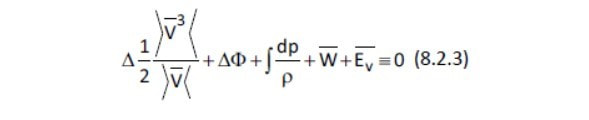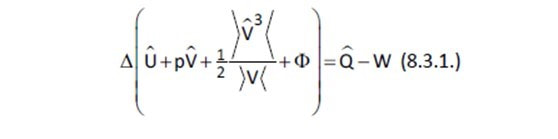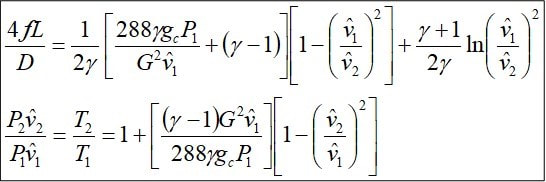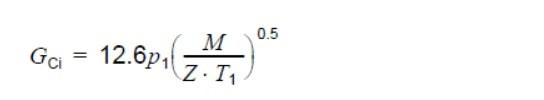MECÁNICA DE FLUIDOS PARA INGENIEROS DE PROCESO.
Por Jaime Santillana y Julia Salinas de Santillana
Ingenieros Químicos (UNI-Perú) M.S.in ChE (University of Wisconsin Madison y University of Illinois at Urbana Champaigne)
www.ssecoconsulting.com
INTRODUCCION
El día 26 de junio, en el Colegio de Ingenieros del Perú, Departamental de Luma, los autores de esta página presentaron su libro
MECÁNICA DE FLUIDOS PARA INGENIEROS DE PROCESO.
La presentación organizada por el Capítulo de Ingeniería Química de Lima, estuvo a cargo del ingeniero Luis Gonzales Talledo.
Se presenta aquí uno de los tópicos del libero Texto y una aplicación del punto planteado.
FLUJO DE FLUIDOS COMPRESIBLES
Tomado del Capítulo III- Fluidos Compresibles del Tópico 8 Flujo de Fluidos Compresibles del Texto Mecánica de Fluidos para Ingenieros de Proceso.
1. INTRODUCCIÓN (1, 2, 3, 4, 7, 8, 19, 20, 80, 81, 82)
El flujo de gases y vapores a través de gasoductos suele ser diferente del flujo de fluidos incompresibles. Esto porque el calor generado por fricción, que es muy pequeño para alterar las propiedades de un fluido incompresible, cambia las propiedades físicas de los gases y vapores.
Una determinación precisa de la caída de presión requerirá conocer la relación exacta entre presión y densidad a lo largo de la tubería y esto no es muy fácil de obtener, ya que de manera general la densidad de gases y vapores varía con la presión y temperatura.
Los gases y vapores se comportan como fluidos politrópicos, siguen la relación P nn = Cte, donde es muy difícil calcular n. Se toman dos límites: flujo isotérmico y flujo adiabático.
Cuando un flujo compresible fluye de una región a alta presión hacia una región de baja presión se expande y disminuye su densidad.
En tuberías de sección transversal constante la disminución de la viscosidad hace necesario que el fluido se acelere para mantener el mismo flujo másico, por consecuencia la energía cinética del fluido aumenta con la caída de presión.
En ambos casos cuando un fluido compresible fluye desde una región a alta presión hacia una región de baja presión se expande y disminuye su densidad. En tuberías de sección transversal constante la disminución en la densidad hace necesario que el fluido se acelere para mantener el mismo flujo másico, por consecuencia la energía cinética del fluido aumenta con la caída de presión.
En el flujo isotérmico en tuberías la densidad varía con la presión mientras que la temperatura se mantiene constante. El flujo isotérmico se representa según: Pn = cte.
Este tipo de flujo se asume para tuberías largas sin aislamiento donde la temperatura del fluido se supone que es la del medio ambiente. El caso más notable lo constituyen los gasoductos.
En flujo adiabático, caracterizado por la ausencia de pérdidas de calor al ambiente, la temperatura disminuye a medida que decrece la presión; lo que trae como resultado el aumento de la densidad. Estos flujos se representan según Png= constante.
Esta situación de flujo adiabático (63) se suele presentar en plantas químicas y refinerías que presentan una gran cantidad de tuberías aisladas (para evitar pérdidas de calor) de longitud relativamente pequeñas (de hasta algunos cientos de metros).
Los flujos reales se encuentran acotados dentro de los flujos isotérmicos y los flujos adiabáticos. Cuando los resultados de estos modelos difieren, suele ocurrir que el modelo isotérmico predice una mayor caída de presión y por lo tanto da un resultado más conservador.
Los flujos reales se encuentran acotados dentro de los flujos isotérmicos y adiabáticos. Cuando los resultados de estos modelos difieren, el modelo isotérmico predice una caída de presión mayor para un flujo másico dado; por lo que el resultado es más conservador.
A la inversa, a una caída de presión constante el modelo adiabático predice un mayor thoroughput y por eso se lo emplea en diseños conservadores.
A elevadas presiones y temperaturas el comportamiento de los gases es no ideal, presentando factores de compresibilidad (Z) menores a la unidad; lo que puede resultar en un flujo adiabático con aumento de la densidad del fluido. Esta condición de altas caídas de presión (DP) en fluidos compresibles suele ocurrir en sistemas de venteo, equipos de destilación al vacío y gasoductos muy extensos.
La determinación del caudal del fluido (Q) o caída de presión (DP) en fluidos compresibles está controlada por la densidad. A medida que la presión disminuye, por las resistencias de tuberías válvulas y accesorios, el gas se expande y su velocidad aumenta (acelerándolo), hasta que se llega a un límite que no puede ser excedido por el gas o vapor (10).
El límite para el flujo de un fluido compresible es la velocidad crítica o velocidad sónica. Aun si la velocidad aguas abajo del ducto es menor que la presión requerida para alcanzar la velocidad sónica, el caudal (o velocidad del fluido) no se llevará por encima de la velocidad calculada para la velocidad crítica.
Por lo tanto, para una caída de presión dada (DP), la masa descargada a través de una tubería con un fluido en flujo adiabático es mayor en un 20% que la masa de descarga para un flujo isotérmico. Esto ocurre con tuberías de hasta aproximadamente 1,000 diámetros de tubería de largo.
2 BALANCES MACROSCÓPICOS DE ENERGÍA MECÁNICA (ECUACIÓN DE BERNOULLI) (2, 3, 4, 7, 8, 12, 19, 20, 80)
Al igual que en 3.5., se mostrarán aquí los balances macroscópicos de energía mecánica tanto para el flujo isotérmico como el adiabático.
FLUJO DE FLUIDOS COMPRESIBLES
Tomado del Capítulo III- Fluidos Compresibles del Tópico 8 Flujo de Fluidos Compresibles del Texto Mecánica de Fluidos para Ingenieros de Proceso.
1. INTRODUCCIÓN (1, 2, 3, 4, 7, 8, 19, 20, 80, 81, 82)
El flujo de gases y vapores a través de gasoductos suele ser diferente del flujo de fluidos incompresibles. Esto porque el calor generado por fricción, que es muy pequeño para alterar las propiedades de un fluido incompresible, cambia las propiedades físicas de los gases y vapores.
Una determinación precisa de la caída de presión requerirá conocer la relación exacta entre presión y densidad a lo largo de la tubería y esto no es muy fácil de obtener, ya que de manera general la densidad de gases y vapores varía con la presión y temperatura.
Los gases y vapores se comportan como fluidos politrópicos, siguen la relación P nn = Cte, donde es muy difícil calcular n. Se toman dos límites: flujo isotérmico y flujo adiabático.
Cuando un flujo compresible fluye de una región a alta presión hacia una región de baja presión se expande y disminuye su densidad.
En tuberías de sección transversal constante la disminución de la viscosidad hace necesario que el fluido se acelere para mantener el mismo flujo másico, por consecuencia la energía cinética del fluido aumenta con la caída de presión.
En ambos casos cuando un fluido compresible fluye desde una región a alta presión hacia una región de baja presión se expande y disminuye su densidad. En tuberías de sección transversal constante la disminución en la densidad hace necesario que el fluido se acelere para mantener el mismo flujo másico, por consecuencia la energía cinética del fluido aumenta con la caída de presión.
En el flujo isotérmico en tuberías la densidad varía con la presión mientras que la temperatura se mantiene constante. El flujo isotérmico se representa según: Pn = cte.
Este tipo de flujo se asume para tuberías largas sin aislamiento donde la temperatura del fluido se supone que es la del medio ambiente. El caso más notable lo constituyen los gasoductos.
En flujo adiabático, caracterizado por la ausencia de pérdidas de calor al ambiente, la temperatura disminuye a medida que decrece la presión; lo que trae como resultado el aumento de la densidad. Estos flujos se representan según Png= constante.
Esta situación de flujo adiabático (63) se suele presentar en plantas químicas y refinerías que presentan una gran cantidad de tuberías aisladas (para evitar pérdidas de calor) de longitud relativamente pequeñas (de hasta algunos cientos de metros).
Los flujos reales se encuentran acotados dentro de los flujos isotérmicos y los flujos adiabáticos. Cuando los resultados de estos modelos difieren, suele ocurrir que el modelo isotérmico predice una mayor caída de presión y por lo tanto da un resultado más conservador.
Los flujos reales se encuentran acotados dentro de los flujos isotérmicos y adiabáticos. Cuando los resultados de estos modelos difieren, el modelo isotérmico predice una caída de presión mayor para un flujo másico dado; por lo que el resultado es más conservador.
A la inversa, a una caída de presión constante el modelo adiabático predice un mayor thoroughput y por eso se lo emplea en diseños conservadores.
A elevadas presiones y temperaturas el comportamiento de los gases es no ideal, presentando factores de compresibilidad (Z) menores a la unidad; lo que puede resultar en un flujo adiabático con aumento de la densidad del fluido. Esta condición de altas caídas de presión (DP) en fluidos compresibles suele ocurrir en sistemas de venteo, equipos de destilación al vacío y gasoductos muy extensos.
La determinación del caudal del fluido (Q) o caída de presión (DP) en fluidos compresibles está controlada por la densidad. A medida que la presión disminuye, por las resistencias de tuberías válvulas y accesorios, el gas se expande y su velocidad aumenta (acelerándolo), hasta que se llega a un límite que no puede ser excedido por el gas o vapor (10).
El límite para el flujo de un fluido compresible es la velocidad crítica o velocidad sónica. Aun si la velocidad aguas abajo del ducto es menor que la presión requerida para alcanzar la velocidad sónica, el caudal (o velocidad del fluido) no se llevará por encima de la velocidad calculada para la velocidad crítica.
Por lo tanto, para una caída de presión dada (DP), la masa descargada a través de una tubería con un fluido en flujo adiabático es mayor en un 20% que la masa de descarga para un flujo isotérmico. Esto ocurre con tuberías de hasta aproximadamente 1,000 diámetros de tubería de largo.
2 BALANCES MACROSCÓPICOS DE ENERGÍA MECÁNICA (ECUACIÓN DE BERNOULLI) (2, 3, 4, 7, 8, 12, 19, 20, 80)
Al igual que en 3.5., se mostrarán aquí los balances macroscópicos de energía mecánica tanto para el flujo isotérmico como el adiabático.
Ambas ecuaciones son muy similares y al ser proceso isoentrópico se tiene que -Q = Ev; es decir, la velocidad de producción de energía calorífica por disipación viscosa es igual a la velocidad de eliminación de calor a través de las paredes del sistema.
En estado estacionario se tendrá lo siguiente:
En estado estacionario se tendrá lo siguiente:
Esta expresión corresponde a la ecuación de Bernoulli. Para evaluar la integral, se deberá conocer una ecuación de estado (r = r(p,T)).
En esta forma de la ecución de Bernoulli no se tomarán en cuenta los fenómenos de aceleración; lo que se verá más adelante.
La ecuación I dp/rho se puede integrar para dos casos sencillos:
En esta forma de la ecución de Bernoulli no se tomarán en cuenta los fenómenos de aceleración; lo que se verá más adelante.
La ecuación I dp/rho se puede integrar para dos casos sencillos:
En gases el número de Reynolds local y el factor de fricción son prácticamente constantes porque las variaciones de viscosidad son muy pequeñas. En cambio, la velocidad media sí puede variar apreciablemente en el ducto.
Cuando la viscosidad o la densidad varían apreciablemente a lo largo de su recorrido, se expresa la ecuación de Bernoulli de manera diferencial y se integra. Las pérdidas por válvulas y accesorios se calculan para flujos subsónicos similarmente a la de los líquidos.
Se ha encontrado que es conveniente efectuar cálculos para flujo compresible empleando el volumen específico vˆ en lugar de la densidad r.
3 FLUJO DE FLUIDOS COMPRESIBLES ADIABÁTICOS (1, 2, 3, 4, 7, 8, 12, 19, 20, 80, 81, 83, 84, 85)
Las plantas químicas y refinerías presentan numerosas tuberías de pequeña longitud. La transferencia de calor es pequeña y el flujo es adiabático.
En el flujo adiabático, a medida que la presión disminuye también lo hace la temperatura; lo que ocasiona que la densidad aumente. A altas presiones y temperaturas el factor de compresibilidad (Z) puede ser menor que 1; lo que también incrementa la densidad del fluido. En los flujos adiabáticos horizontales se emplea el balance macroscópico de energía en estado estacionario:
Cuando la viscosidad o la densidad varían apreciablemente a lo largo de su recorrido, se expresa la ecuación de Bernoulli de manera diferencial y se integra. Las pérdidas por válvulas y accesorios se calculan para flujos subsónicos similarmente a la de los líquidos.
Se ha encontrado que es conveniente efectuar cálculos para flujo compresible empleando el volumen específico vˆ en lugar de la densidad r.
3 FLUJO DE FLUIDOS COMPRESIBLES ADIABÁTICOS (1, 2, 3, 4, 7, 8, 12, 19, 20, 80, 81, 83, 84, 85)
Las plantas químicas y refinerías presentan numerosas tuberías de pequeña longitud. La transferencia de calor es pequeña y el flujo es adiabático.
En el flujo adiabático, a medida que la presión disminuye también lo hace la temperatura; lo que ocasiona que la densidad aumente. A altas presiones y temperaturas el factor de compresibilidad (Z) puede ser menor que 1; lo que también incrementa la densidad del fluido. En los flujos adiabáticos horizontales se emplea el balance macroscópico de energía en estado estacionario:
En este caso para flujo adiabático `Q = 0, además W = 0.
Como el flujo suele ser altamente turbulento, se puede emplear la siguiente aproximación:
Como el flujo suele ser altamente turbulento, se puede emplear la siguiente aproximación:
y luego diferenciarla y suponer que no hay trabajo; además, si la tubería es horizontal Z2 = Z1. En estas condiciones la ecuación de Bernoulli diferencial puede ser expresada según:
Para gases ideales PV = RT, por lo que:
Reemplazando esta expresión en 8.3.16. y manipulando algebraicamente se obtiene:
Las expresiones 8.3.20. y 8.3.22. describen un flujo adiabático en una tubería horizontal.
Conocido el flujo y la presión aguas arriba se requiere calcular la caída de presión
Las ecuaciones 8.3.20. y 8.3.24. se pueden expresar en unidades inglesas según:
Conocido el flujo y la presión aguas arriba se requiere calcular la caída de presión
Las ecuaciones 8.3.20. y 8.3.24. se pueden expresar en unidades inglesas según:
Donde:
D = diámetro tubería en pies f = factor fricción
G = velocidad másica en lbm/pie2xseg L = longitud tubería en pie
T = temperatura en ºR gc = 32.17 lbf/lbmxpie/seg2
vi = volumen específico pie3/lbm γ = cp /cv
Nota: en estas ecuaciones se expresa P1 en psi y se multiplica por 144 para que las unidades estén expresadas en lbf/pie2.
Conocida la caída de presión aguas arriba se requiere estimar el flujo
T. W. Cochran (81) propuso una metodología específica mostrada en el Texto.
.......
Consideraciones adicionales.-
Es posible mostrar que a medida que la presión cae aumenta el caudal del gas transportado, existiendo una condición de flujo máximo que corresponde al flujo crítico o flujo en condiciones de shock. Existe una máxima caída de presión que da el máximo flujo másico y corresponde al número de Mach; es decir, cuando la velocidad del fluido compresible se acerca a la velocidad del fluido que se está transportando. Por esta razón, Cochran (69) y Lapple (67) presentan una metodología de cálculo de flujos compresibles adiabáticos considerando la posibilidad de la existencia de la barrera denominada velocidad del sonido.
Estas condiciones de flujos sónicos deben basarse en situaciones físicas donde existe una gran caída de presión, como sistemas de venteo, topes de columnas de destilación a vacío, equipos de descarga a la atmósfera por razones de seguridad: válvulas de escape, válvulas de alivio, tanques de los denominados knock out drum, etc.
4. MÉTODO DETALLADO DE LAPPLE PARA FLUJO ADIABÁTICO (1, 4, 83, 84)
Las ecuaciones presentadas en 8.3. no tienen soluciones sencillas. Por este motivo aún algunos ingenieros siguen empleando el método gráfico que fuera desarrollado por Lapple en 1943 (83, 84).
El método, tal como se presenta aquí, es válido para tuberías horizontales y considera tres casos diferentes:
- Conocido el flujo y la presión aguas arriba se quiere calcular la caída de presión.
- Conocido el flujo y la presión aguas abajo se quiere calcular la caída de presión.
- Conocida la caída de presión se quiere calcular el flujo másico.
Conocido el flujo y la presión aguas arriba se quiere calcular la caída de presión:
Si N > 400, se debe dividir la tubería en secciones de menor longitud, y se deberá calcular la caída de presión de cada tramo individual, empezando de la zona de aguas arriba; d viene expresado en pulgadas.
Recuerde que: DP/P1 = (P1 - P2)/P1
D = diámetro tubería en pies f = factor fricción
G = velocidad másica en lbm/pie2xseg L = longitud tubería en pie
T = temperatura en ºR gc = 32.17 lbf/lbmxpie/seg2
vi = volumen específico pie3/lbm γ = cp /cv
Nota: en estas ecuaciones se expresa P1 en psi y se multiplica por 144 para que las unidades estén expresadas en lbf/pie2.
- Se calcula la velocidad másica por unidad de área (G).
- Se calcula el número de Reynolds en las condiciones de entrada.
- Se calcula el factor de fricción con las condiciones de entrada.
- Con (i) se halla el valor de v2.
- Con (ii) se halla P2.
- Se debe verificar que V2; es decir, que el flujo es subsónico.
- Si (-ΔP)/P1 es mucho mayor a 10% se debe ir por tramos cortos.
Conocida la caída de presión aguas arriba se requiere estimar el flujo
T. W. Cochran (81) propuso una metodología específica mostrada en el Texto.
.......
Consideraciones adicionales.-
Es posible mostrar que a medida que la presión cae aumenta el caudal del gas transportado, existiendo una condición de flujo máximo que corresponde al flujo crítico o flujo en condiciones de shock. Existe una máxima caída de presión que da el máximo flujo másico y corresponde al número de Mach; es decir, cuando la velocidad del fluido compresible se acerca a la velocidad del fluido que se está transportando. Por esta razón, Cochran (69) y Lapple (67) presentan una metodología de cálculo de flujos compresibles adiabáticos considerando la posibilidad de la existencia de la barrera denominada velocidad del sonido.
Estas condiciones de flujos sónicos deben basarse en situaciones físicas donde existe una gran caída de presión, como sistemas de venteo, topes de columnas de destilación a vacío, equipos de descarga a la atmósfera por razones de seguridad: válvulas de escape, válvulas de alivio, tanques de los denominados knock out drum, etc.
4. MÉTODO DETALLADO DE LAPPLE PARA FLUJO ADIABÁTICO (1, 4, 83, 84)
Las ecuaciones presentadas en 8.3. no tienen soluciones sencillas. Por este motivo aún algunos ingenieros siguen empleando el método gráfico que fuera desarrollado por Lapple en 1943 (83, 84).
El método, tal como se presenta aquí, es válido para tuberías horizontales y considera tres casos diferentes:
- Conocido el flujo y la presión aguas arriba se quiere calcular la caída de presión.
- Conocido el flujo y la presión aguas abajo se quiere calcular la caída de presión.
- Conocida la caída de presión se quiere calcular el flujo másico.
Conocido el flujo y la presión aguas arriba se quiere calcular la caída de presión:
- El diámetro o el diámetro equivalente si la tubería no es de sección circular.
- El número de Reynolds a partir del flujo másico y los datos disponibles.
- El factor de fricción f de alguna expresión apropiada.
- El factor de resistencia de la tubería N, a partir de:
Si N > 400, se debe dividir la tubería en secciones de menor longitud, y se deberá calcular la caída de presión de cada tramo individual, empezando de la zona de aguas arriba; d viene expresado en pulgadas.
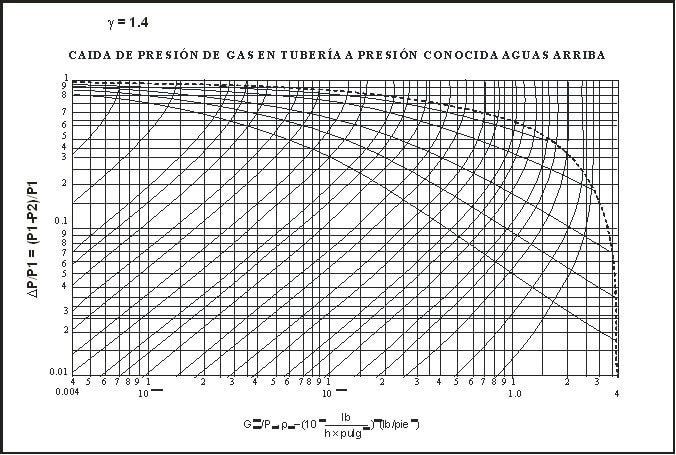
- Se calcula el término Gh2 / P1r1 , donde P1 es la presión aguas arriba y r1 es la densidad aguas arriba. En las gráficas de Lapple adjuntas, la velocidad másica Gh se expresa en Mlbm/hrxpulg2; P1 se expresa en psia y la densidad ρ se expresa en lbm/pie3.
- Halle el valor de g (relación calor específico a presión constante a calor específico a volumen constante Cp/Cv). Trabaje con g = 1.4 en las gráficas que se adjuntan.
- Encuentre DP/P1 de las figuras 8.1. Interpole linealmente en la figura adjunta.
Recuerde que: DP/P1 = (P1 - P2)/P1
Fig. 8.1. Gráfico de Lapple para caídas de presión cuando se conoce la presión aguas arriba y g = Cp / Cv = 1.4
Si Gh2/P1 r1 cae por debajo del rango cubierto por las figuras, el fluido es incompresible y se pueden aplicar las técnicas descritas en capítulos anteriores.
}Si Gh2/P1 r1 cae en la parte vertical de las curvas para N en las figuras 8.1., la velocidad del gas en la tubería será sónica. Entonces, la caída de presión tendrá dos contribuciones: la caída de presión hasta alcanzar el flujo sónico y la caída de presión a través de la onda de choque a la salida de la tubería, según:
DPT = DP línea + DP onda de choque
Si Gh2/P1r1 cae más allá de la parte vertical de las curvas para N en la figura 8.1., existirá una situación física imposible. Para que exista una solución posible se deberá elevar la presión aguas arriba (P1) o se deberá aumentar el tamaño de la tubería.
Conocido el flujo y la presión aguas abajo se quiere calcular la caída de presión:
Continua en el Texto.
……
Otras consideraciones de diseño.-
Cuando la caída de presión por fricción y aceleración, calculada para tuberías horizontales (por cualquiera de los métodos señalados), es pequeña ̶como por ejemplo ocurre en chimeneas̶ se debe considerar adicionalmente el cambio de presión por diferencia de alturas. Para ello se emplea la ecuación de Bernoulli.
Cuando se quiere calcular el flujo másico a una caída de presión conocida, primero se debe restar el DP por altura del DP total dado. Luego, se procede de acuerdo con el método de Lapple.
Cuando los sistemas adiabáticos incluyen orificios, nozzles, boquillas, se debe proceder a calcular el DP en cada uno de ellos. Si el sistema es complejo, este se deberá dividir en diversas secciones. Algunas de estas secciones contendrán un solo equipo (orificio, nozzles, venturi). En otros casos las secciones podrán incluir tramos de tuberías y algunos accesorios.
De cualquier manera, se deberá empezar a calcular la caída de presión para cada sección empezando del final de la tubería donde se asume que la presión es conocida. Las caídas de presión de cada tramo se evalúan como se ha descrito. Los codos y las válvulas se toman en cuenta añadiendo los coeficientes de resistencia para hallar nuevos valores de N. Cada vez que se tenga una válvula se analiza la posibilidad de flujo sónico. Si esto ocurre, se trata la válvula como un nozzle.
El anexo n° 7 presenta los diversos valores de g (Cp/Cv) para diversos gases a 68 ºF y 14.7 psia. Los valores varían desde 1.67 para gases como el helio y el argón; 1.4 para gases diatómicos, como el hidrógeno, dióxido de carbono, nitrógeno y pueden tener valores aun menores para gases con mayor peso molecular.
5.- APLICACIÓN DEL METODO DE LAPPLE – API 521
Depressuring Systems (Ver http://www.fakels.ru/wp-content/uploads/2017/08/api_std_521_2014_6th_edition_pressure_relieving_and_depressu.pdf)
Una aplicación del Método de Lapple se encuentra en el API 521 que trae la siguiente secuencia de cálculo. (Traducción libre de los autores)
5.5 Método de Lapple para el cálculo de la caída de presión
En el resto de esta sección, se ofrece una solución rápida para dimensionar líneas donde se reduce la presión, utilizando el método desarrollado por Lapple [101].
Este método emplea un flujo de masa crítico teórico basado en una boquilla ideal y un flujo adiabático, condiciona y asume una presión de fuente conocida de baja velocidad aguas arriba. El flujo de masa crítica para el flujo isotérmico pára gases donde el vapor k = Cp / Cv = 1.00. Aquí se puede determinar utilizando la Ecuación (37):
Si Gh2/P1 r1 cae por debajo del rango cubierto por las figuras, el fluido es incompresible y se pueden aplicar las técnicas descritas en capítulos anteriores.
}Si Gh2/P1 r1 cae en la parte vertical de las curvas para N en las figuras 8.1., la velocidad del gas en la tubería será sónica. Entonces, la caída de presión tendrá dos contribuciones: la caída de presión hasta alcanzar el flujo sónico y la caída de presión a través de la onda de choque a la salida de la tubería, según:
DPT = DP línea + DP onda de choque
Si Gh2/P1r1 cae más allá de la parte vertical de las curvas para N en la figura 8.1., existirá una situación física imposible. Para que exista una solución posible se deberá elevar la presión aguas arriba (P1) o se deberá aumentar el tamaño de la tubería.
Conocido el flujo y la presión aguas abajo se quiere calcular la caída de presión:
Continua en el Texto.
……
Otras consideraciones de diseño.-
Cuando la caída de presión por fricción y aceleración, calculada para tuberías horizontales (por cualquiera de los métodos señalados), es pequeña ̶como por ejemplo ocurre en chimeneas̶ se debe considerar adicionalmente el cambio de presión por diferencia de alturas. Para ello se emplea la ecuación de Bernoulli.
Cuando se quiere calcular el flujo másico a una caída de presión conocida, primero se debe restar el DP por altura del DP total dado. Luego, se procede de acuerdo con el método de Lapple.
Cuando los sistemas adiabáticos incluyen orificios, nozzles, boquillas, se debe proceder a calcular el DP en cada uno de ellos. Si el sistema es complejo, este se deberá dividir en diversas secciones. Algunas de estas secciones contendrán un solo equipo (orificio, nozzles, venturi). En otros casos las secciones podrán incluir tramos de tuberías y algunos accesorios.
De cualquier manera, se deberá empezar a calcular la caída de presión para cada sección empezando del final de la tubería donde se asume que la presión es conocida. Las caídas de presión de cada tramo se evalúan como se ha descrito. Los codos y las válvulas se toman en cuenta añadiendo los coeficientes de resistencia para hallar nuevos valores de N. Cada vez que se tenga una válvula se analiza la posibilidad de flujo sónico. Si esto ocurre, se trata la válvula como un nozzle.
El anexo n° 7 presenta los diversos valores de g (Cp/Cv) para diversos gases a 68 ºF y 14.7 psia. Los valores varían desde 1.67 para gases como el helio y el argón; 1.4 para gases diatómicos, como el hidrógeno, dióxido de carbono, nitrógeno y pueden tener valores aun menores para gases con mayor peso molecular.
5.- APLICACIÓN DEL METODO DE LAPPLE – API 521
Depressuring Systems (Ver http://www.fakels.ru/wp-content/uploads/2017/08/api_std_521_2014_6th_edition_pressure_relieving_and_depressu.pdf)
Una aplicación del Método de Lapple se encuentra en el API 521 que trae la siguiente secuencia de cálculo. (Traducción libre de los autores)
5.5 Método de Lapple para el cálculo de la caída de presión
En el resto de esta sección, se ofrece una solución rápida para dimensionar líneas donde se reduce la presión, utilizando el método desarrollado por Lapple [101].
Este método emplea un flujo de masa crítico teórico basado en una boquilla ideal y un flujo adiabático, condiciona y asume una presión de fuente conocida de baja velocidad aguas arriba. El flujo de masa crítica para el flujo isotérmico pára gases donde el vapor k = Cp / Cv = 1.00. Aquí se puede determinar utilizando la Ecuación (37):
Donde:
GCi es el flujo de masa crítica, expresado en kg / s · m2 (lb / s · ft2);
p1 es la presión absoluta en la fuente de baja velocidad corriente arriba (ver Figura 4), expresada en kPa (psi);
M es la masa molecular relativa del vapor;
T1 es la temperatura aguas arriba, expresada en K (° R);
Z es el factor de compresibilidad, adimensional.
El factor de compresibilidad se debe tomar en condiciones de flujo y, por lo tanto, cambia a medida que el fluido se mueve hacia abajo en la línea con
Una caída de presión resultante. Se puede emplear un cálculo por pasos para permitir esta variación. Una solución precisa
el uso de este método es tedioso, pero generalmente se pueden obtener resultados suficientemente precisos al realizar el cálculo
en incrementos relativamente grandes de longitudes de tubería, utilizando un factor de compresibilidad promedio en esas longitudes.
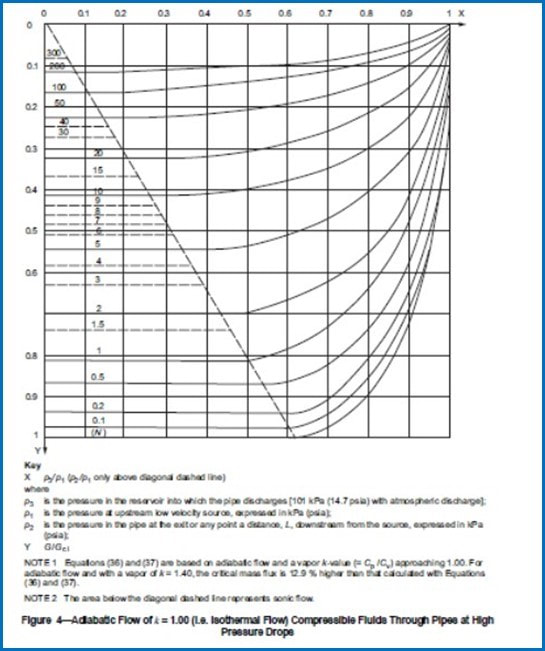
Independientemente de la ecuación utilizada, el flujo de masa real (G) es una función del flujo de masa crítica (GCi), resistencia de fricción (N), y la relación entre la presión corriente abajo y la presión corriente arriba. Estas relaciones se representan en la Figura 4. (Gráficos similares para Lapple [101] ha desarrollado casos adiabáticos con proporciones de calores específicos de 1.4 y 1.8.) En el área a continuación en la línea diagonal de la Figura 4, la relación G / GCi permanece constante, lo que indica que se ha establecido el flujo sónico.
La resistencia de fricción total para usar con el gráfico se expresa mediante la Ecuación (38):
GCi es el flujo de masa crítica, expresado en kg / s · m2 (lb / s · ft2);
p1 es la presión absoluta en la fuente de baja velocidad corriente arriba (ver Figura 4), expresada en kPa (psi);
M es la masa molecular relativa del vapor;
T1 es la temperatura aguas arriba, expresada en K (° R);
Z es el factor de compresibilidad, adimensional.
El factor de compresibilidad se debe tomar en condiciones de flujo y, por lo tanto, cambia a medida que el fluido se mueve hacia abajo en la línea con
Una caída de presión resultante. Se puede emplear un cálculo por pasos para permitir esta variación. Una solución precisa
el uso de este método es tedioso, pero generalmente se pueden obtener resultados suficientemente precisos al realizar el cálculo
en incrementos relativamente grandes de longitudes de tubería, utilizando un factor de compresibilidad promedio en esas longitudes.
Independientemente de la ecuación utilizada, el flujo de masa real (G) es una función del flujo de masa crítica (GCi), resistencia de fricción (N), y la relación entre la presión corriente abajo y la presión corriente arriba. Estas relaciones se representan en la Figura 4. (Gráficos similares para Lapple [101] ha desarrollado casos adiabáticos con proporciones de calores específicos de 1.4 y 1.8.) En el área a continuación en la línea diagonal de la Figura 4, la relación G / GCi permanece constante, lo que indica que se ha establecido el flujo sónico.
La resistencia de fricción total para usar con el gráfico se expresa mediante la Ecuación (38):
Donde
- N es el factor de resistencia de fricción de la tubería, adimensional;
- f es el factor de fricción de Moody, adimensional;
- l es la longitud real de la tubería, expresada en m (pies);
- d es el diámetro del tubo, expresado en m (pies);
- Ki son los coeficientes de resistencia de los accesorios, adimensionales.
NOTA DE LOS AUTORES
Si encuentran interesantes y útiles los artículos presentados en nuestra página web, una manera de apoyar su continuidad y expansión es mediante la adquisición de este Texto.
En caso de tener interés de adquirir el Texto favor contactarnos a jaime.santillanasoto@gmail.com
JS /JS
Julio 2019
Si encuentran interesantes y útiles los artículos presentados en nuestra página web, una manera de apoyar su continuidad y expansión es mediante la adquisición de este Texto.
En caso de tener interés de adquirir el Texto favor contactarnos a jaime.santillanasoto@gmail.com
JS /JS
Julio 2019